我好难啊奥数难题关卡中需要玩家解开如果鸡界穿裤子,以下哪一个是答案,本站带来我好难啊奥数难题详细策略,希望可以帮到大家。
我好难啊奥数难题详细策略

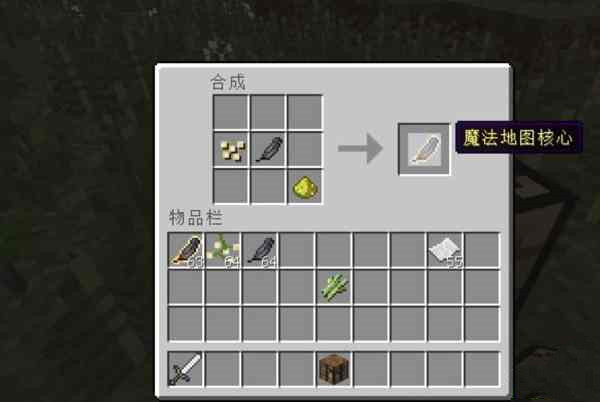
1、首先玩家到达这个关卡然后了解到这个任务,需要先点击C尾巴,把D和C合成、A和B合成、DC和AB都合成。
2、先是点击C号鸡的尾巴会掉落出篮球,然后在将D号鸡和C号鸡合成。
3、这边是需要将A和B号鸡合成,然后在将俩只剩余的鸡一起合成,最后就是只有一只鸡和一个篮球。
4、玩家只需要等待一会,可以发现鸡会打篮球了,最后获得本关的胜利。
奥数难题,急需0
是不是弄错了?
带帽子的与带手套和围巾的人同样多?
这个是什么意思? 是:1、 戴帽子的=戴手套的+戴围巾的?
还是:2、 戴帽子的=戴手套的=戴围巾的?
如果是1,则设总人数为a,则a-4=a-8+a-7,则a=11,算下去,跟题目给的条件不符。
如果是2,明显与条件:不戴帽子的有4个,没带手套的有8个,没戴围巾的有7个,不符。
超难奥数题
啃数论书,听课,狂做题。别无选择。
做的多了,拿到题目就会有思路,知道从哪个方面考虑,用哪些定理。许多数论题目的某一部分总是相似的,方法也大同小异。
建议先看小丛书,然后啃奥赛经典。啃完奥赛经典数论水平就接近顶尖了,不要放弃,加油。数论一直是我的弱项,我有个同学数论超猛就是基本做完了一本奥赛经典,但是这次数论太水他挂了。还是要全面发展,平几的分也是比较好拿的。
小学奥数超难题 数学高手快来挑战
1正数是两个。
如果是3个,那么由(1/x)+(1/y)+(1/z)=1,知道x,y,z,均大于1,
但是与1/(x+y+z)=1矛盾,所以不可能有3个。
如果是1个正数,不妨设为x>0,y<0,z<0,由1/(x+y+z)=1即x+y+z=1
x>1, 1/x<1, 1/y<0, 1/z<0
这样与(1/x)+(1/y)+(1/z)=1,矛盾
所以正数为2个
2设a=b=c=t,t不为0,由立方项系数为0,所以a+b+c+d=0,d=-3t
所以方程可以写成(x-t)^3(x+3t)=0
比较系数得到,r=-3t^4, q=8t^3,p=-6t^2
仅有p+q=r时,有实数解,所以真命题有1个
3 个位是4或者6
4p=-(a+b),q=ab,所以p-q>-3,有 -(a+b)-ab>-3
有-(1+a)b>a-3
b<-(a-3)/(a+1)=(3-a)/(a+1)
而a>1,有0<3-a<a+1
(3-a)/(a+1)<1
所以b<(3-a)/(a+1)<1
b<1
5
(x-5)^2+(y+5)^2=50
m=x-5,n=y+5
m^2+n^2=50
就是求mn有多少正数解。
m=正负1时候,n=正负7,四组
m=2,3,4时候,无解
m=正负5时候,n=正负5,四组
m=正负6时候无解
m=正负7时候,n=正负1,四组
一共12组正数解
6
71+2++n=n(n+1)/2
[(1^2)+(2^2)++(n^2)]=n(n+1)(2n+1)/6
[(1^3)+(2^3)++(n^3)]=[n(n+1)]^2/4
[(1^4)+(2^4)+(3^4)++(n^4)]=SN=
(1+n)^5=n^5+5n^4+10n^3+10n^2+5n+1
(1+n-1)^5=(n-1)^5+5(n-1)^4+10(n-1)^3+10(n-1)^2+5(n-1)+1
(1+1)^5=1^5+51^4+101^3+101^2+51+1
以上n个式子求和
(1+n)^5=1^5 +5SN+10[n(n+1)]^2/4+10n(n+1)(2n+1)/6+5n(n+1)/2+N
[(1^4)+(2^4)+(3^4)++(100^4)]/[(1^2)+(2^2)++(100^2)]=60598
小学六年级奥数题 要难的 ,有解的
选A
我高三,这种题很简单。
解释一下:规定a>0则a^x>0,指数函数的图像过一、二象限
y=a^x是y=loga x的反函数,关于y=x对称
则对数函数的图像过一、四象限。
六年级奥数精选
我的孩子也六年级,下面的题都是我精选出来的(我自己多年辅导小学奥数)。题不要多,要让孩子做一道,明白一个系列。一共有5份,这是其中的一份。但愿对您的孩子有点帮助。我的邮箱dfacs@163com
1某水池可以用甲、乙两水管注水,单放甲管需12小时注满,单放乙管需24小时注满。现在规定10小时内必须注满水池,那么甲、乙两管同时注水时间至少要几小时?
解析:把工作总量看作单位“1”,甲管的工效为1/12,乙管的工效为1/24,甲管的工效更高。
10小时注满,要使两管同时注水时间尽可能少,应把工效高的甲管开满10小时,不足部分由乙管注入,乙管注水时间就是两管同开时间,两管同时注水时间最少为:
(1-10×1/12)÷1/24=4(小时)
2一个水池,甲、乙两管同时开,5小时灌满;乙、丙两管同时开,4小时灌满。如果乙管先开6小时,还需要甲、丙两管同时开2小时才能灌满(这时乙管关闭),那么乙管单独灌满水池需要多少小时?
解析:把灌满一池水的工作量看作单位“1”,则甲、乙两管同开的工效为1/5,乙、丙两管同开的工效为1/4。 “乙管先开6小时,甲、丙两管再同时开2小时”,相当于甲、乙先同开2小时,乙、丙再同开2小时,最后乙再单独开2小时。 根据以上分析,可以先求出乙管单独开2小时的工作量:
1-2×1/5-2×1/4=1/10再根据工作时间与工作量的比例关系,求出乙管单独灌满水池需要的时间:2÷(1-2×1/5-2×1/4)=20(小时)。
3一个水池安装了甲、乙两根进水管,在同样的时间内,乙管的进水量是甲管的16倍。为了灌满空着的水池,开始由甲管灌入1/5池水,然后关闭甲管,打开乙管,由乙管单独灌满剩下的水,共用12分15秒,问甲管开了多长时间?
解析:12分15秒=49/4分钟 把灌满一池水的工作量看作单位“1”,乙管所灌的剩下的水量为:1-1/5=4/5 “同样的时间内,乙管的进水量是甲管的16倍。”即乙管的工效是甲管的16倍。工作量一定,工效和工作时间成反比,可以推出灌满一池水甲管所用的时间是乙管的16倍。假设乙管灌满一池水需要x分钟,则甲管需要16x分钟,由题意可得:16x×1/5+x×4/5=49/4解得:x=175/16所以甲管的开放时间为:16×(175/16)×1/5=35(分钟)
4蓄水池装有甲、丙两根进水管和乙、丁两根排水管。要注满一池水,单开甲管要3小时,单开丙管要5小时。要排光,单开乙管要4小时,单开丁管要6小时。现知池内有1/6池水,如果按甲、乙、丙、丁、甲、乙、丙、丁的顺序轮流开1小时,问多长时间后,水开始溢出水池?
解析:4个小时一个周期,先求出一个循环周期的进水量情况:
第1个小时后,水池中存水量增加:1/3
每4个小时后,水池中存水量增加:1/3-1/4+1/5-1/6=7/60
分析上面的情况,每个周期水池的水量会增长7/60,但只要水池中不足水量为不超过1/3,即水量达到2/3,在下一个周期里,就可以直接由甲管注满。
池中已有水量为1/6,且空出1/3的容积:
(1-1/6-1/3)÷7/60=4又2/7
即需要5个周期后水池的水量才能达到2/3,。
第6个周期的进水量情况:
需要注入水量:1-1/6-5×7/60=1/4
甲管还需要注水时间:1/4÷1/3=3/4(小时)
所以,从开始到水溢出共需时间:4×5+3/4=20又3/4(小时)
5兄妹两人同时从家出发去1080米远的学校上学,哥哥骑车每分钟走360米,妹妹步行每分钟走60米,哥哥到校门口时,发现忘带课本,立即原路返回,问哥哥再次由家出发在离学校多远处追上妹妹?
解析:哥哥比妹妹总共多行了家与学校之间全程的2倍,即(1080×2)米。而哥哥每分钟比妹妹多行(360-60)米。则从兄妹同时出发到哥哥再次追及妹妹,经过时间为:
1080×2÷(360-60)=72(分钟)。用家校距离减去妹妹行走路程,可以求出追及地点离学校的距离为:1080-72×60=648(米)。
7实验小学组织学生排队步行去郊游,步行速度是每秒1米,排头的王老师以每秒25米的速度赶到排尾,然后立即返回排头,共用10分钟,求队伍的长度。
第一次排头的王老师从排头赶到排尾的过程中,王老师步行的路程与队伍步行路程之和正好等于队伍的长度;
第二次王老师从排尾赶到排头,王老师步行路程与队伍步行路程之差正好等于队伍的长度。
解法一,假设王老师从排头赶到排尾用了x分钟,由题意可得:
(1+25)×60x=(25-1)×60×(10-x)
解得:x=3
所以,队伍的长度为:
(1+25)×60×3=630(米)
解法二:令王老师从排头赶到排尾的时间为第一段时间,这段时间里,王老师和队伍步行的路程和等于队伍长度,即:
队伍长度=(1+25)×第一段步行时间
令王老师从排尾赶到排头的时间为第二段时间,这段时间里,王老师和队伍步行的路程差等于队伍长度,即:
队伍长度=(25-1)×第二段步行时间
队伍长度是一定的,速度与时间成反比例,即速度扩大几倍,时间就缩小相同的倍数。
(1+25)÷(25-1)=7/3
所以第一段时间是第二段时间的3/7,是总时间的3/10。
所以队伍的长度为:
(1+25)×60×(10×3/10)=630(米)
6甲从A地步行去B地,同时乙从B地骑自行车去A地,1小时后在途中第一次相遇。乙到达A地后立即返回到B地,在途中又追上了甲,此时与第一次相遇相隔40分钟,乙到达B地后又立即折返A地,两人又第二次相遇在途中,此时与乙追上甲的时间相隔多长?
第一次相遇时,两人合行了1个全程,需要1小时。第二次相遇时,两人合行了3个全程,则需要3个小时。即第二次相遇与出发时间相隔3个小时。
乙追上甲时,与出发时间相隔:1小时+40分钟=1小时40分钟。
所以,两人第二次相遇时与乙追上甲的时间相隔:3小时-1小时40分钟=1小时20分钟